Hack into the system
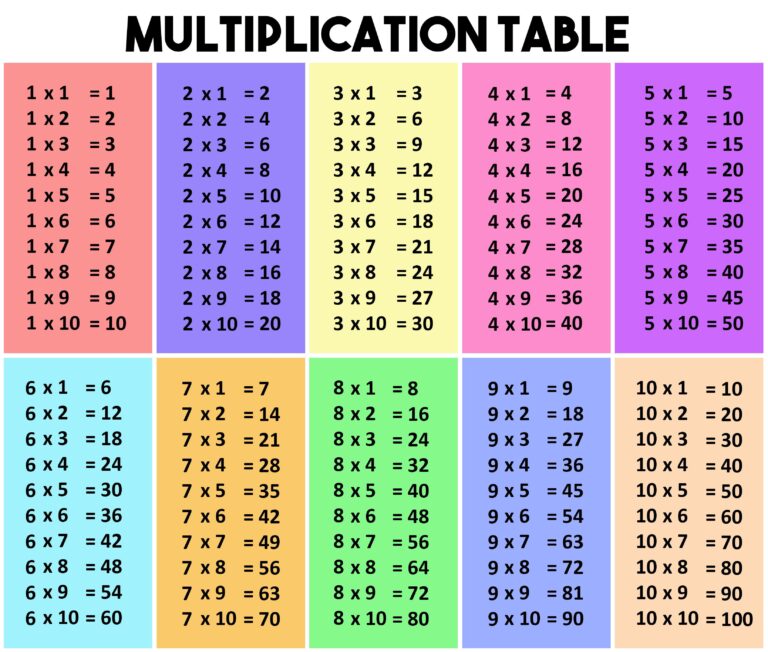
Usually the multiplication table on the back of school notebooks looks like this.
How to learn the multiplication table: the multiplication table on notebooks.
One kind of endless columns with numbers can drive an energetic junior high into despair. So no doubt take the fat marker and cross out the mathematical torture in front of your child. This is not just a performance, but a way to create a positive mood. Instead of complicated examples, offer the schoolboy the Pythagoras table.
How to learn the multiplication table: the Pythagoras table…
This is the real multiplication table. Show the child how easy it is to use.The result of multiplying two digits is a number that is at the intersection of a row and a column with the corresponding digits. For example, to multiply 3 by 4, it is sufficient to draw two lines in your mind: one horizontal from the digit 3 in the left column, and the second vertical from the digit 4 in the top row. The result is 12.
Explain that the task is twice as easy as it seems.
Multiply 3 by 4 together. Now ask your child to change the numbers: choose 3 not in a vertical column, but in a horizontal row. And 4, respectively, in the column on the left. Please note that the result will be the same. And 3 × 4, and 4 × 3 equals 12. How to help the child learn the multiplication table: explain the commutation property
Multiplication Games for 3rd Grade: Ditching the Flashcards. Or as a child’s language, “change in the places of multipliers does not change the result”. You don’t have to remember how much 3 × 4 or 4 × 3 will be. It is enough to learn that numbers 3 and 4 in any order when multiplying by each other give 12. A simple conclusion from the switchability property follows. The multiplication table is half the size and simpler than it seems. If you know how many 4 × 7 will be, then you automatically know how many 7 × 4 will be. You don’t have to teach it anymore.
Help the child understand the physical meaning of multiplication.
You can do this by drawing rectangles on the table with the sides corresponding to the multiplied figures.
For example, this is how you can show what 2 × 4 is – two rows of four cells in each. How to learn the multiplication table quickly: count the number of cells Invite your child to calculate how many cells fit in the resulting rectangle. That way, he’ll find that 2 × 4 = 8.
Scan or print several copies of the Pythagoras table and together with the student draw other rectangles – horizontal, vertical, small and large, counting how many cells they contain. In this way you also use the visual memory: remembering how many there will be, for example, 3 × 4, the child will imagine the corresponding figure – and easily answer.
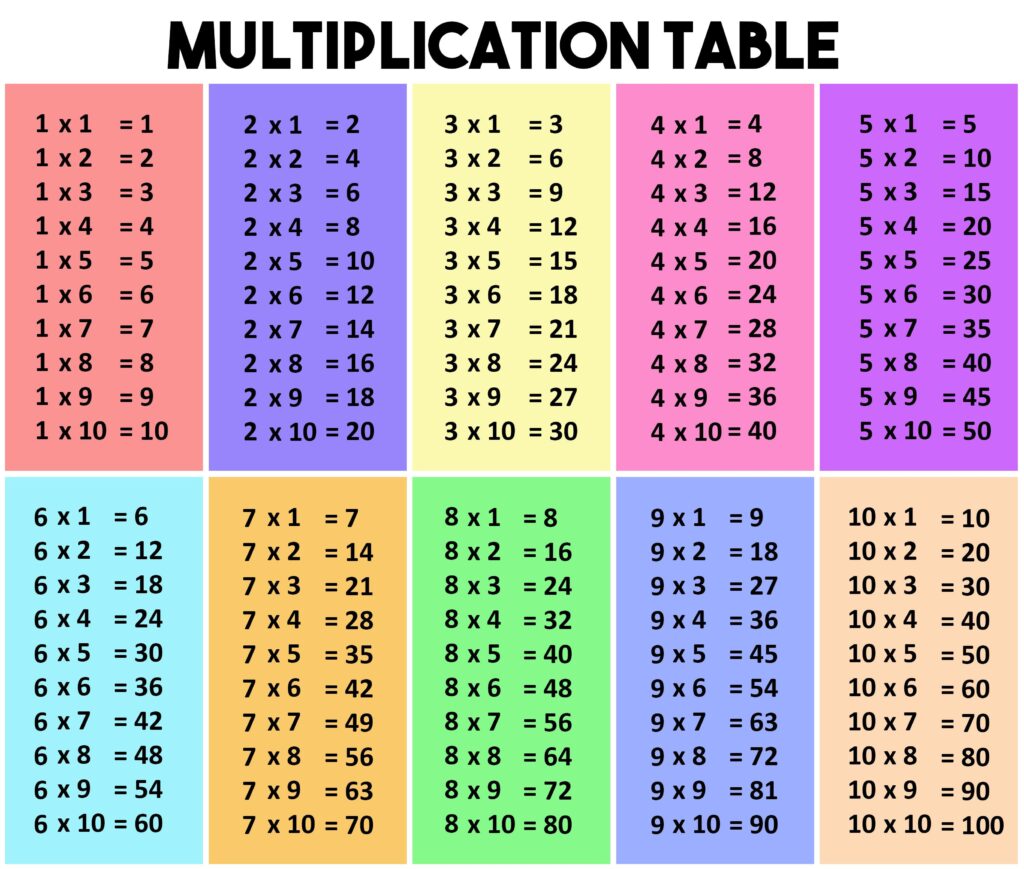
Find the patterns in the table.
When a child discovers a pattern for himself, he remembers it forever. This is a simpler and more effective way to learn the multiplication table than rote.
These are some of the patterns that are worth looking at.
- When multiplied by 1, any number remains the same.
- Multiplication by 2 is just a number to which the same number is added. For example, 3 × 2 means 3 has been added to 3. 8 × 2 means 8 + 8.
- All examples multiplied by 5 have a result that ends in 5 or 0.
- To multiply by 5 any even number, you should take a half of it and attribute 0 to it. For example, 6 × 5: take a half of 6 is number 3 – and add zero to it: it turns out 30.
- At multiplication by 9 the sum of figures as a result will certainly be equal to 9. For example, 2 × 9 = 18 (1 + 8 = 9). 3 × 9 = 27 (2 + 7 = 9). And so on.
- To multiply any number by 10, you just need to add zero to the right of it.
Learn in small portions
You don’t have to try to squeeze everything out in one sitting. Start by multiplying by 1, 2, and 3 and dedicate a day or two to each such topic. This will gradually prepare your child to learn more complex information.
When a student has learned the simplest columns, move on to the more complex numbers, first multiplying by 4-7 and then multiplying by 8-9.
Repeat
The more often, the better. Ask in order first, and when the answers are sure, you’ll get an increase. Keep an eye on the pace as well: Allow more time for reflection at first, but gradually ask your child to answer faster.
Print or buy training posters
It’s better a few. Hang them in those places where the child spends a lot of time – in the children’s (play) area, above the desk, on the fridge.
Posters should be large and bright. You can also use those that do not show the Pythagoras table, but standard examples. In any case, the child will cling to the colorful image and it will be fixed in the memory.